Nanomagnetism & Oxides Laboratory
Magnetic vortex dynamics
People: G. de Loubens (Permanent staff) 
Alumni: B. Pigeau (PhD)
Collaborations: 
Fundings: ANR VOICE (2009-2012) et TOPSKY (2017-2020)
The magnetic vortex is a topological singularity which can be stabilized in thin ferromagnetic platelets due to the competition between demagnetizing and exchange energies. This micromagnetic state can be viewed as an in-plane curling magnetization with a central region, the vortex core, where the magnetization points out-of-plane. The vortex state is characterized by two topological quantities: the vortex core polarization (direction of the vortex core magnetization) and the vortex chirality (rotational direction of the in-plane magnetization). The main originality of our studies on vortex dynamics in magnetic dots lies in the fact that a bias field normal to the sample plane is applied. This induces a deformation of the vortex texture into the so-called “cone state”, and correspondingly, of its topology, which modifies its linear excitation spectrum [1,2] (cf. Fig.1). Moreover, it is also interesting to spectroscopically investigate the nonlinearities of the gyrotropic mode, and how the dynamical reversal of the vortex core is affected by the presence of the perpendicular bias field [3]. In our studies, we use MRFM to detect the magnetization dynamics in individual soft magnetic dots with high dynamical quality. In particular, we show that the applied perpendicular field lifts the frequency degeneracy of the gyrotropic modes associated to opposite core polarities p = ±1, which allows a simple spectroscopic determination of the core orientation with respect to the bias field [4], and enables deterministic dynamical reversal of the vortex core [5]. Moreover, taking advantage of the strayfield of the MRFM probe, we determine the anharmonicity of the magnetostatic confinement potential of the vortex core in a nanodot [6] (cf. Fig.2). An important aspect of our work on magnetic vortex dynamics in individual nanodisks is that it has strong connections with our research activities on vortex-based spin torque oscillators, where applying a perpendicular field and determining nonlinearities are crucial, and on magnetic skyrmions, which are other non-trivial topological textures appearing in magnetic materials with strong Dzyaloshinskii-Moriya interaction, which favors chiral configurations of the magnetization.
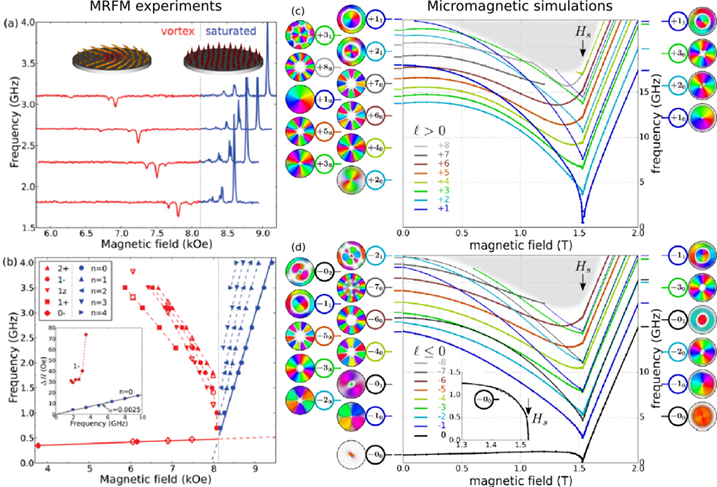
Fig.1. Spin-wave modes in the cone state. (a) MRFM spectra obtained on an individual disk of NiMnSb of diameter 1 µm. (b) Dispersion relation of the different spin-wave modes observed experimentally. (c), (d) Micromagnetic simulation of the spin-wave spectra as a function of the perpendicular field Hz. Modes are labeled using their azimuthal and radial indices. The two panels differentiate spin-waves depending on their sense of gyration. Their spatial profiles in the vortex (µ0Hz=0 T) and saturated states (µ0Hz=2 T) are shown on the left and right sides, respectively.
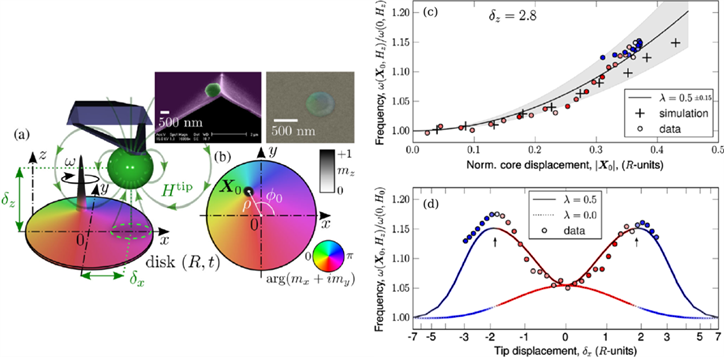
Fig.2. MRFM spectroscopy of the vortex core confinement potential. (a) Side and (b) top views of the experimental setup:the stray field of the MRFM tip is used to displace the static position of the vortex core. (c) Plot of the relative variation of eigenfrequency of the gyrotropic mode as a function of the latter. (d) Relative variation of the eigenfrequency as a function of the tip displacement. The lines show the analytical behaviors for a vanishing and a finite anharmonic coefficient.
References:
[1] V. Castel, J. Ben Youssef, F. Boust, R. Weil, B. Pigeau, G. de Loubens, V. V. Naletov, O. Klein, N. Vukadinovic, Perpendicular ferromagnetic resonance in soft cylindrical elements: Vortex and saturated states, Phys. Rev. B 85, 184419 (2012). 
[2] B. Taurel, T. Valet, V. V. Naletov, N. Vukadinovic, G. de Loubens, O. Klein, Complete mapping of the spin-wave spectrum in a vortex-state nanodisk, Phys. Rev. B 93, 184427 (2016). 
[3] B. Pigeau, G. de Loubens, O. Klein, A. Riegler, F. Lochner, G. Schmidt, L.W. Molenkamp, Optimal control of vortex-core polarity by resonant microwave pulses, Nature Phys., 7, 26–31 (2011). 
[4] G. de Loubens, A. Riegler, B. Pigeau, F. Lochner, F. Boust, K. Y. Guslienko, H. Hurdequint, L. W. Molenkamp, G. Schmidt, A. N. Slavin, V. S. Tiberkevich, N. Vukadinovic, O. Klein, Bistability of Vortex Core Dynamics in a Single Perpendicularly Magnetized Nanodisk, Phys. Rev. Lett. 102, 177602 (2009). 
[5] B. Pigeau, G. de Loubens, O. Klein, A. Riegler, F. Lochner, G. Schmidt, L.W. Molenkamp, V.S. Tiberkevich, A.N. Slavin, A frequency-controlled magnetic vortex memory, Appl. Phys. Lett. 96, 132506 (2010). 
[6] O. V. Sukhostavets, B. Pigeau, S. Sangiao, G. de Loubens, V. V. Naletov, O. Klein, K. Mitsuzuka, S. Andrieu, F. Montaigne, K. Y. Guslienko, Probing the Anharmonicity of the Potential Well for a Magnetic Vortex Core in a Nanodot, Phys. Rev. Lett. 111, 247601 (2013).